Wing Bending, Torsion, and Shear Analysis Program
Project Overview
This MATLAB-based analysis tool evaluates structural performance of aircraft wings under combined torsion, bending, and shear loads. It enables rapid assessment of wing structural integrity, providing key insights into stress distribution, deflection, and safety margins for conceptual and preliminary design phases.
How the Code Works
User Inputs:
• Wing geometry (span, chord, airfoil thickness, spar/rib layout)
• Material properties (Young’s modulus, shear modulus, density)
• Applied loading conditions (lift distribution, shear forces, torsional moments, and bending moments)
Analysis Modules:
-
Bending Analysis
• Computes bending stress distribution using beam theory.
• Determines maximum deflection and stress along the span.
-
Shear Analysis
• Calculates shear flow and shear stresses in wing spars and skin panels.
• Evaluates load paths through multi-cell wing box structures.
-
Torsional Analysis
• Solves for twist distribution along the wing span.
• Accounts for warping constraints and stiffness of closed vs. open sections.
Outputs:
• Stress and deflection plots across the span.
• Shear flow distribution and torsional twist results.
• Structural safety checks based on material limits and user-defined safety factors.
Impact
This program streamlines early-stage wing structural analysis, eliminating manual calculations and providing a reusable framework for rapid design iteration. It demonstrates proficiency in structural mechanics, MATLAB programming, and aerospace system design.
Diagram of Wing profile
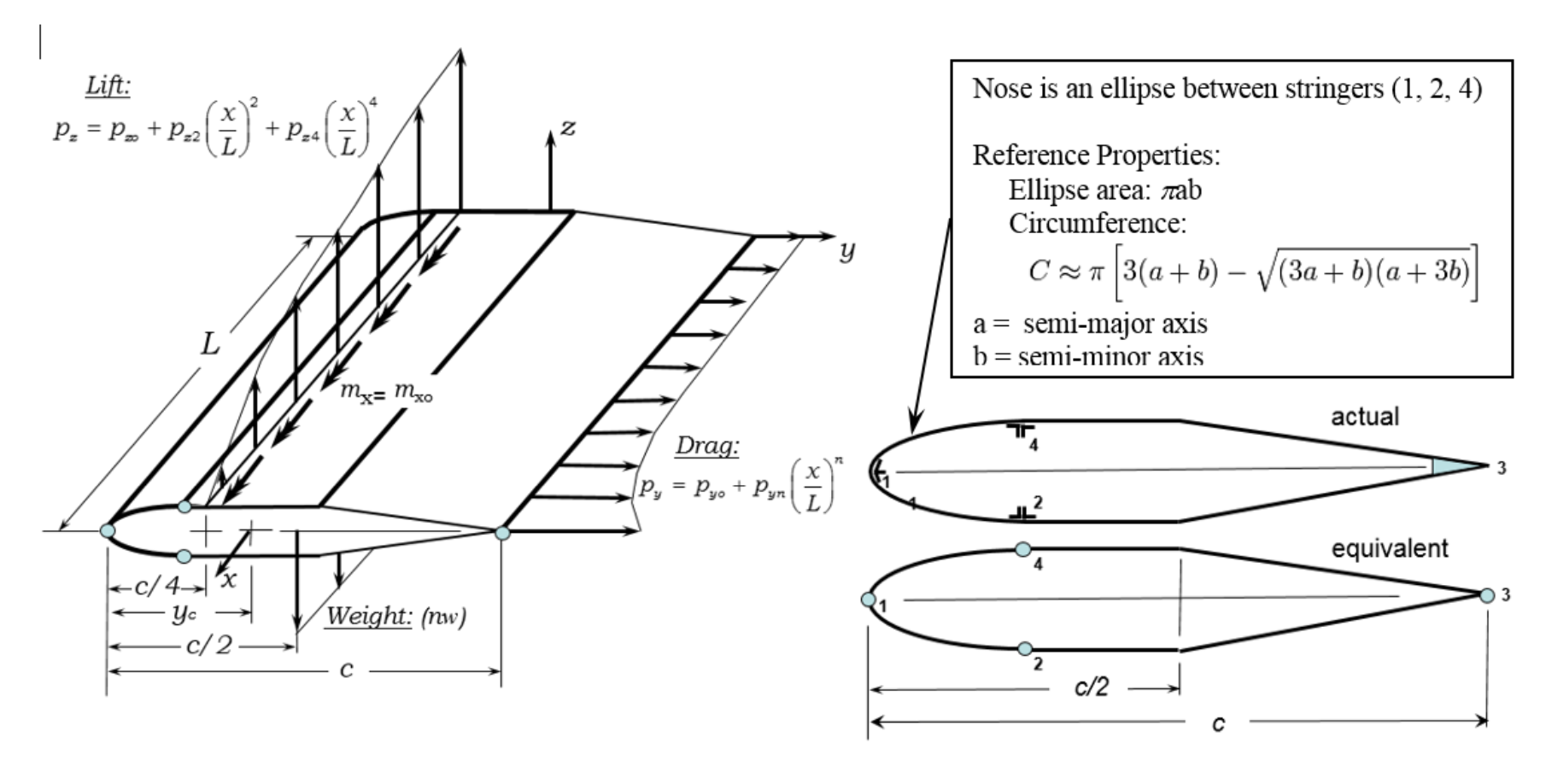
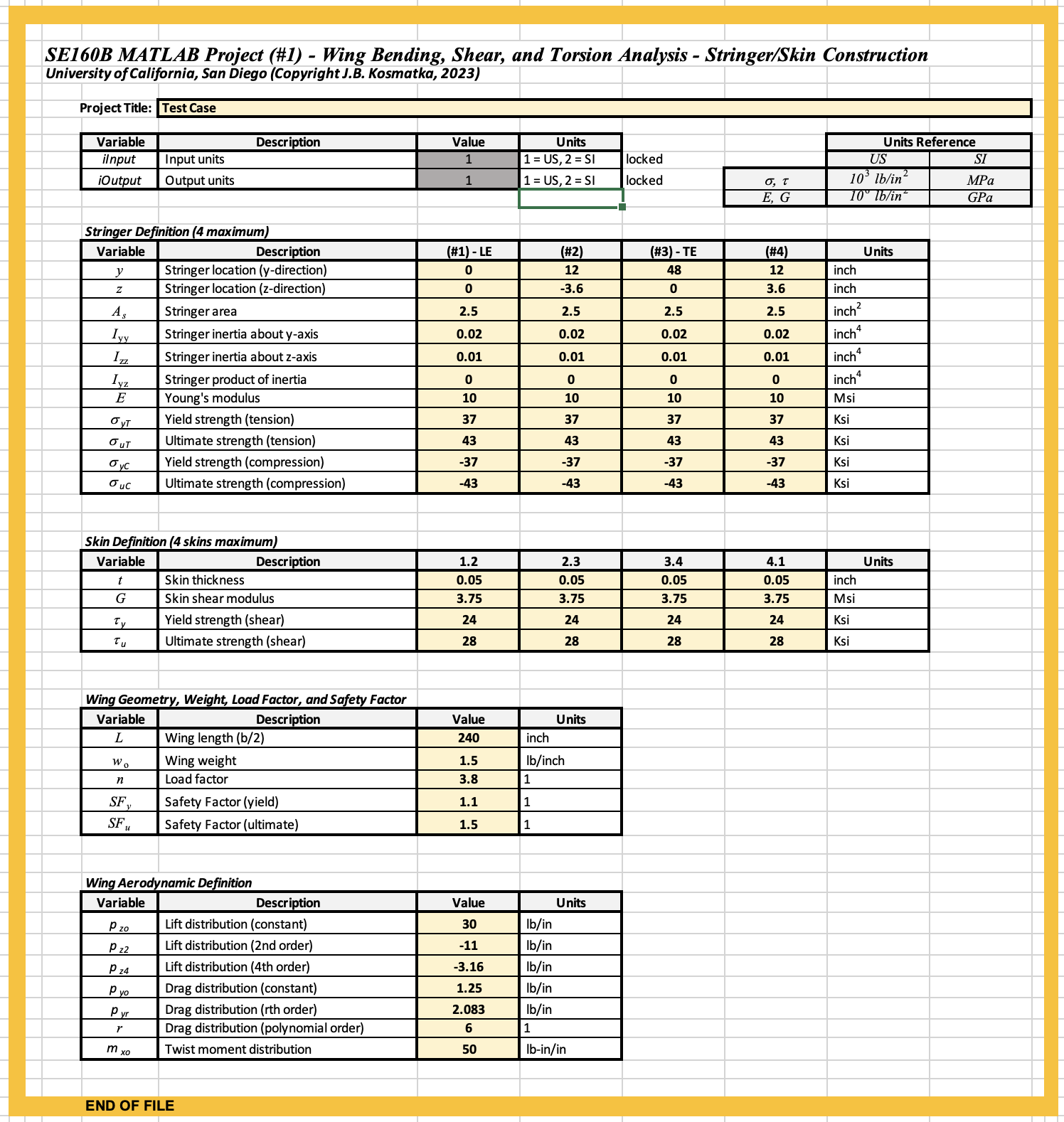
Sample input file
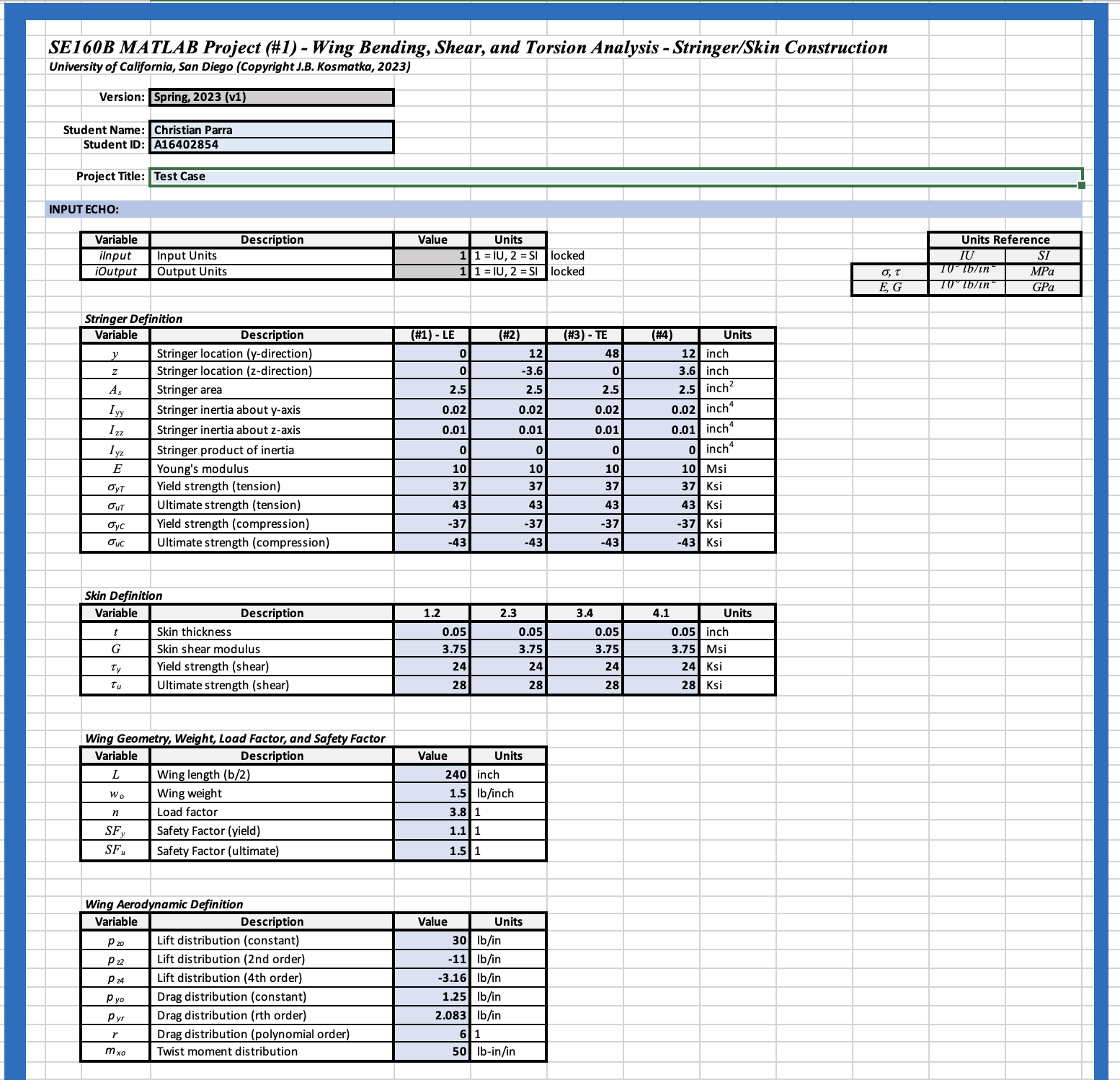
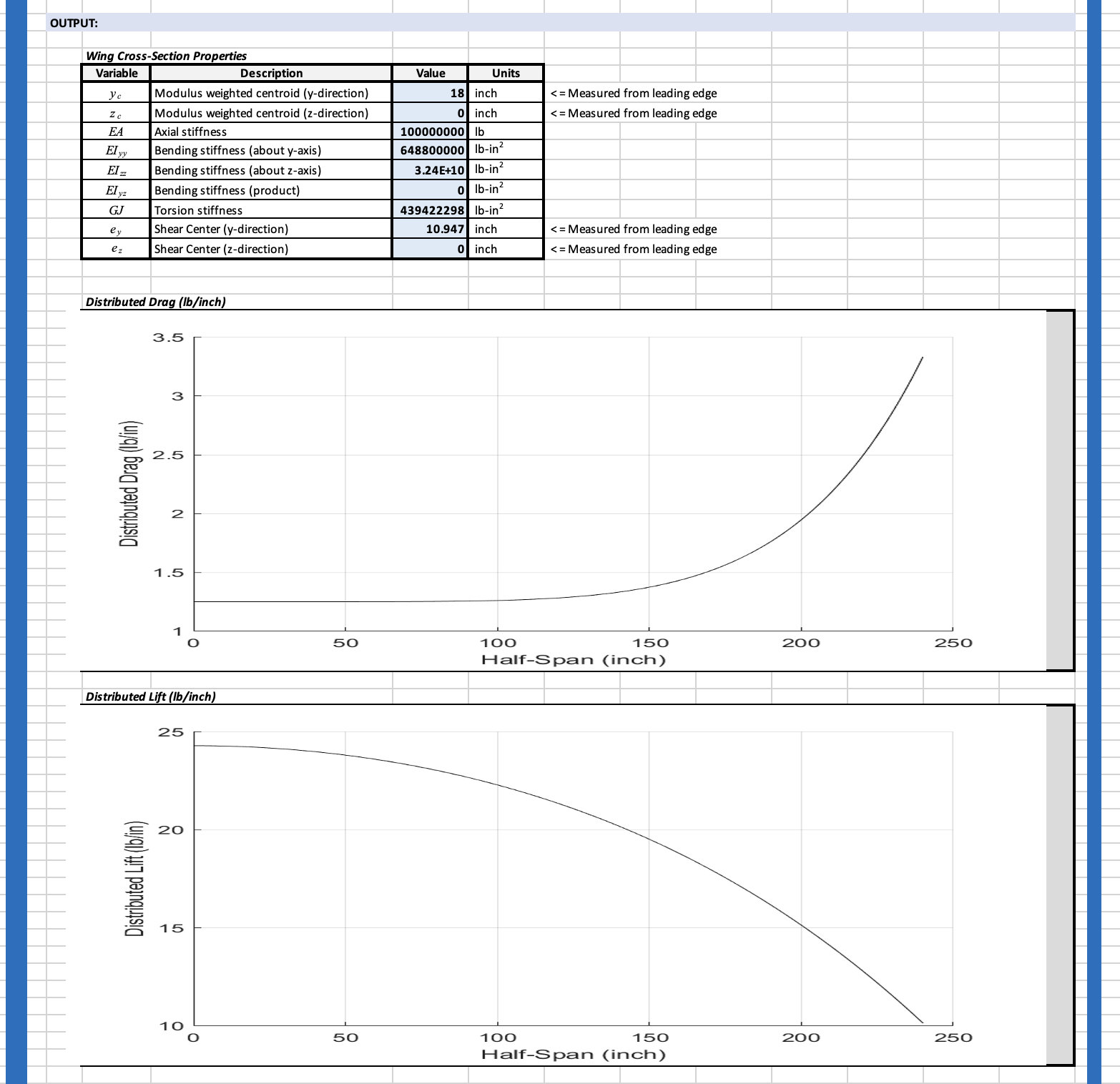
Sample output file
Project MATLAB Code (click to expand)
function result = SE160B_1_Wing_Analysis_Function(inFile, outFile, ...
stringerDef, skinDef,wingDef, wingAero)
% + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
% +
% + SE-160B: Aerospace Structural Analysis II
% +
% + Title: wingAnalysis
% + Author: Christian Parra
% + PID: A16402854
% + Revised: 04/16/2023
% +
% + This function performs a complete analysis of a nontapered symmetric
% + wing having a single cell and four stringers. The skin is divided
% + into four segments. The analysis includes:
% +
% + A) SECTION PROPERTIES
% + A.1) Modulus Centroid Location (yc, zc)
% + A.2) Section Properties (EIyy, EIzz, EIyz)
% + A.3) Torsion Constant (GJ)
% + A.4) Shear Center (ey, ez)
% + B) LOADS
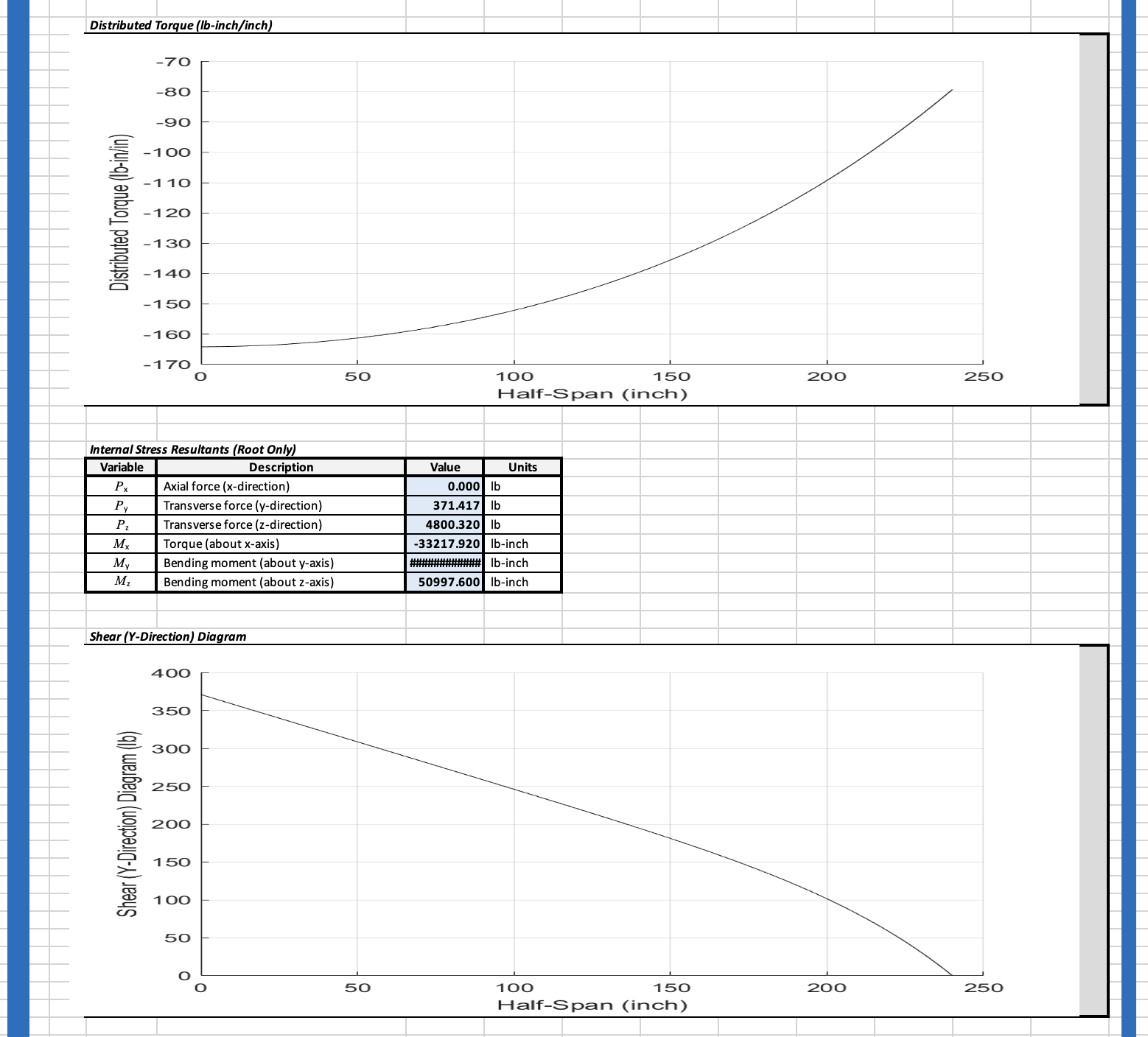
% + B.1) Distributed load plotting (Py, Pz, Mx)
% + B.2) Wing Root Resultants (Vyo, Vzo, Mxo, Myo, Mzo)
% + B.3) Internal Shear and Moment Diagrams (Vy, Vz, Mx, My, Mz)
% + C) INTERNAL STRESSES
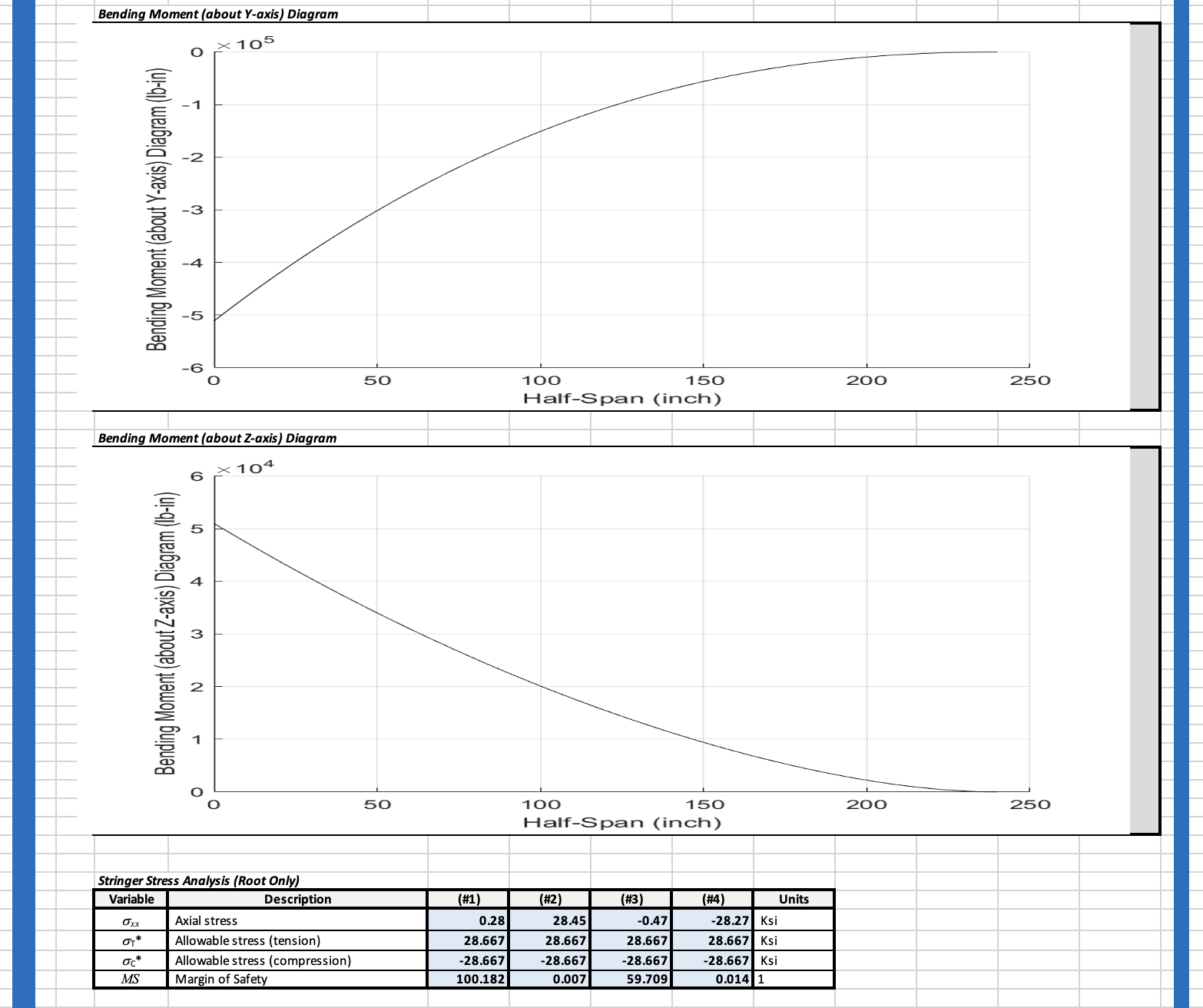
% + C.1) Root Stringer Stress (sxx) and MS
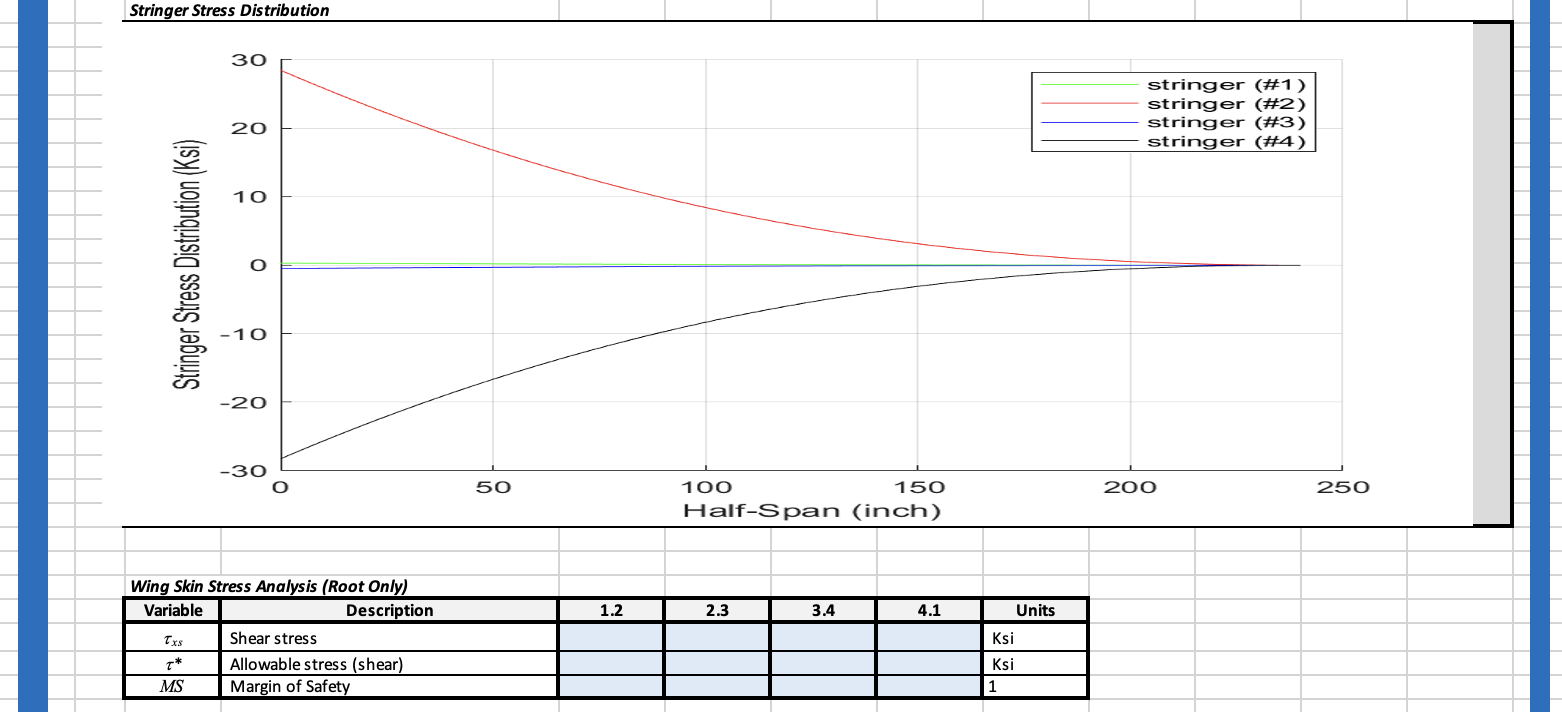
% + C.2) Skin Shear Stress (tau-xs and MS)
% + D) WING TIP DISPLACEMENTS AND TWIST
% + D.1) Plot of wing lift displacement
% + D.2) Plot of wing drag displacement
% + D.3) Plot of wing twist rotation
% + D.4) Calculated wing tip displacement and twist rotation
% +
% + Input:
% + outfile Name of Excel output file
% + stringerDef Properties of four stringers. Matrix (11,4)
% + skinDef Properties of four skin panels Matrix (4,4)
% + wingDef Properties of symmetric one-cell wing (5,1)
% + wingAero Properties of the wing aero loads (7,1)
% + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + +
% Define author name, PID, and program version number
name = {'Christian Parra'};
PID = {'A16402854'};
version = {'Spring, 2023 (v1)'};
% Write program version, author, PID
xlswrite(outFile, version , 1, 'F7' ); % Write Version
xlswrite(outFile, name , 1, 'F9' ); % Write Name
xlswrite(outFile, PID , 1, 'F10'); % Write PID
% Extract stringer property definition
for i = 1:4;
Ys(i) = stringerDef( 1,i); % Stringer y locations
Zs(i) = stringerDef( 2,i); % Stringer z locations
As(i) = stringerDef( 3,i); % Stringer Area
Iyys(i) = stringerDef( 4,i); % Stringer Iyy
Izzs(i) = stringerDef( 5,i); % Stringer Izz
Iyzs(i) = stringerDef( 6,i); % Stringer Iyz
Es(i) = stringerDef( 7,i)*(1000000.); % Stringer Young's Modulus (psi)
SyTs(i) = stringerDef( 8,i)*(1000.); % Stringer Yield Tension (psi)
SuTs(i) = stringerDef( 9,i)*(1000.); % Stringer Ultimate Tension (psi)
SyCs(i) = stringerDef(10,i)*(1000.); % Stringer Yield Compression (psi)
SuCs(i) = stringerDef(11,i)*(1000.); % Stringer Ultimate Compression (psi)
end
% Extract skin definition
for i = 1:4
T_sk(i) = skinDef( 1,i); % Skin thickness
G_sk(i) = skinDef( 2,i)*(1000000.); % Sin shear modulus (Msi to psi)
tau_y_sk(i) = skinDef( 3,i)*(1000.); % Skin shear strength (yield)
tau_u_sk(i) = skinDef( 4,i)*(1000.); % Skin shear strength (ultimate)
end
% Extract wing geometry, weight, load factor, and safety factor
L = wingDef(1); % Wing Length (inch)
ws = wingDef(2); % Wing Weight (lb/inch)
nLF = wingDef(3); % Load Factor (1)
SFy = wingDef(4); % Safety Factor (yield)
SFu = wingDef(5); % Safety Factor (ultimate)
chord = (Ys(3)-Ys(1)); % Wing chord (inch)
% Extract wing aerodynamic definition
pz0 = wingAero(1); % Lift distribution (constant) (lb/in)
pz2 = wingAero(2); % Lift distribution (2nd order) (lb/in)
pz4 = wingAero(3); % Lift distribution (4th order) (lb/in)
py0 = wingAero(4); % Drag distribution (xonstant) (lb/in)
pyr = wingAero(5); % Drag distribution (rth order) (lb/in)
rth = wingAero(6); % Drag distribution (polynomial order) (1)
mx0 = wingAero(7); % twist moment distribution (constant) (lb-in/in)
% Wing Crossection Properties
Yc = sum(Ys.*As.*Es)/sum(As.*Es); % Modulus weighted centroid (y-direction)
Zc = sum(Zs.*As.*Es)/sum(As.*Es); % Modulus weighted centroid (z-direction)
EA = sum(Es.*As); % Axial stiffness
EIyy = sum(Es.*Iyys)+sum(Es.*As.*(Zs-Zc).^2); % Bending stiffness (about y-axis)
EIzz = sum(Es.*Izzs)+sum(Es.*As.*(Ys-Yc).^2); % Bending stiffness (about z-axis)
EIyz = sum(Es.*Iyzs)+sum(Es.*As.*(Ys-Yc).*(Zs-Zc)); % Bending stiffness (product)
%% Torsion Stiffness (GJ)
c=Ys(3)-Ys(1);
compare_c=Ys(2)-Ys(1);
if compare_c<=c/2
%% Ellipse (1 of 3)
a_e = abs(Ys(2)-Ys(1));
b_e = abs(Zs(2)-Zs(1));
A_e = pi/2*a_e*b_e;
S_e = pi/2*(3*(a_e+b_e)-sqrt((3*a_e+b_e)*(a_e+3*b_e)));
%% Square (2 of 3)
a_s = c-c/2-a_e;
b_s = b_e;
A_s = a_s*2*b_s;
S_s = a_s;
%% Triangle (3 of 3)
A_t = c/2*b_s;
S_t = sqrt((c/2)^2+b_s^2);
% Sum of all sections
%defining middle areas from mid point inbetween stringers 2 & 4
A = [A_e/2 A_s/2+A_t/2 A_s/2+A_t/2 A_e/2];
S = [S_e/2 S_s+S_t S_s+S_t S_e/2];
else
%% Ellipse
a_e = abs(Ys(2)-Ys(1));
b_e = abs(Zs(2)-Zs(1));
A_e = pi/2*a_e*b_e;
S_e = pi/2*(3*(a_e+b_e)-sqrt((3*a_e+b_e)*(a_e+3*b_e)));
%%triangle
a_t = abs(Ys(3)-Ys(2));
b_t = abs(Zs(2)-Zs(1));
A_t = a_t*b_t/2;
S_t = sqrt(a_t^2+b_t^2);
% Sum of all sections
A = [A_e/2 A_t A_t A_e/2];
S = [S_e/2 S_t S_t S_e/2];
end
GJ=4*sum(A)^2/sum(S./G_sk./T_sk);
% Load Distributions
px = @(x) 0;
py = @(x) py0+pyr.*(x./L).^rth;
pz = @(x) pz0+pz2.*(x./L).^2+pz4.*(x./L).^4-ws.*nLF;
mx = @(x) -(pz0+pz2.*(x./L).^2+pz4.*(x./L).^4).*(Yc-c./4)-(py0+pyr.*(x./L).^rth).*(Zs(1)-Zc)-ws.*nLF.*(c./2-Yc)+mx0;
my = 0;
mz = 0;
Rox = 0;
Roy = integral(py,0,L);
Roz = integral(pz,0,L);
myo = @(x) -(pz0+pz2.*(x./L).^2+pz4.*(x./L).^4-ws.*nLF).*x;
mzo= @(x) (py0+pyr.*(x./L).^rth).*x;
Mxo = integral(mx,0,L);
Myo = integral(myo,0,L);
Mzo = integral(mzo,0,L);
ISR_Root = [Rox; Roy; Roz; Mxo; Myo; Mzo];
% Shear Center
Kyy = EIyy/(EIyy*EIzz-EIyz^2);
Kyz = EIyz/(EIyy*EIzz-EIyz^2);
Kzz = EIzz/(EIyy*EIzz-EIyz^2);
%defining areas from
K_n1 = [2.*A;1 -1 0 0;0 1 -1 0;0 0 1 -1];
VzEIYY = (Roz*Kzz+Roz*Kyz)*...
[0;...
Es(2)*As(2)*(Zs(2)-Zc);...
Es(3)*As(3)*(Zs(3)-Zc);...
Es(4)*As(4)*(Zs(4)-Zc)];
VyEIZZ = -(Roy*Kyy+Roy*Kyz)*...
[0;...
Es(2)*As(2)*(Ys(2)-Yc);...
Es(3)*As(3)*(Ys(3)-Yc);...
Es(4)*As(4)*(Ys(4)-Yc)];
syms ey
Vzey = Roz*ey*[1; 0 ;0; 0];
q_1234_ey = inv(K_n1)*VzEIYY+inv(K_n1)*Vzey;
ey_string = double(solve((0==1/(2*sum(A))*(sum(q_1234_ey'.*S./G_sk./T_sk))),ey));
ey_final = Ys(2)+ey_string;
syms ez
Vyez = Roy*ez*[1; 0 ;0; 0];
q_1234_ez = inv(K_n1)*VyEIZZ+inv(K_n1)*Vyez;
ez_final = double(solve(0==1/(2*sum(A))*(sum(q_1234_ez'.*S./G_sk./T_sk))));
WCSP = [Yc;Zc;EA;EIyy;EIzz;EIyz;GJ;ey_final;ez_final];
% Distributed lift drag and torque plots
figure(101)
clf
hold on
grid on
fplot(py,[0 L])
xlabel('Half-Span (inch)')
ylabel('Distributed Drag (lb/in)')
figure(102)
clf
hold on
grid on
fplot(pz,[0 L])
xlabel('Half-Span (inch)')
ylabel('Distributed Lift (lb/in)')
syms x
figure(103)
clf
hold on
grid on
fplot(mx,[0 L])
xlabel('Half-Span (inch)')
ylabel('Distributed Torque (lb-in/in)')
%figure 201
Ry= Roy -int(py,0,x);
figure(201)
clf
hold on
grid on
fplot(Ry,[0 L])
xlabel('Half-Span (inch)')
ylabel('Shear (Y-Direction) Diagram (lb)')
%figure 202
Rz= Roz -int(pz,0,x);
figure(202)
clf
hold on
grid on
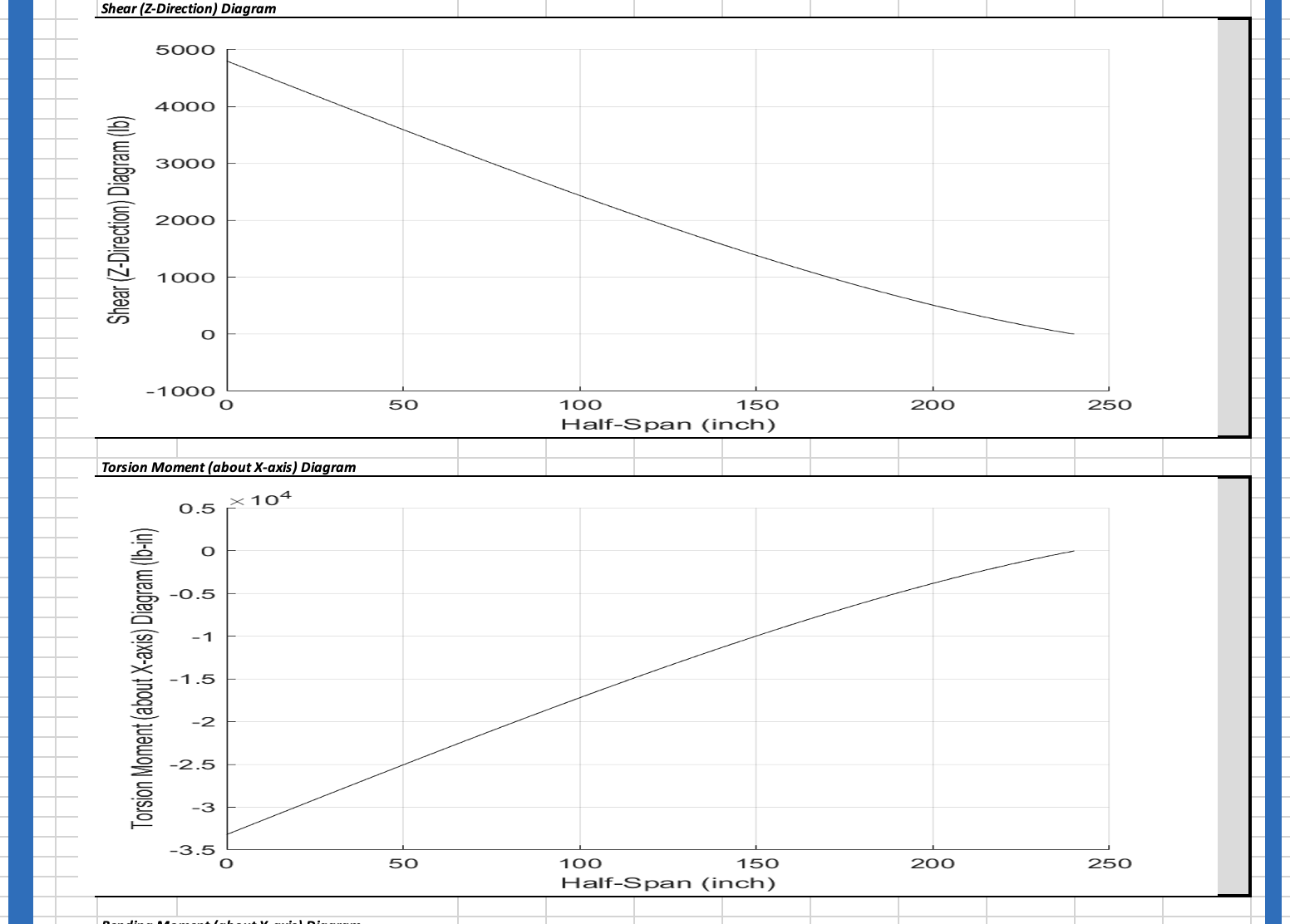
fplot(Rz,[0 L])
xlabel('Half-Span (inch)')
ylabel('Shear (Z-Direction) Diagram (lb)')
%figure 203
Mx= Mxo -int(mx,0,x);
figure(203)
clf
hold on
grid on
fplot(Mx,[0 L])
xlabel('Half-Span (inch)')
ylabel('Torsion Moment (about X-axis) Diagram (lb-in)')
syms x
%figure 204
My= Myo +int( Roz -int(pz,0,x),0,x);
figure(204)
clf
hold on
grid on
fplot(My,[0 L])
xlabel('Half-Span (inch)')
ylabel('Bending Moment (about Y-axis) Diagram (lb-in)')
%figure 205
Mz= Mzo -int( Roy -int(py,0,x),0,x);
figure(205)
clf
hold on
grid on
fplot(Mz,[0 L])
xlabel('Half-Span (inch)')
ylabel('Bending Moment (about Z-axis) Diagram (lb-in)')
%stringer stress
figure(301)
clf
hold on
grid on
for i=1:4
Sxx(i)=Es(i)/1000*[1 -(Ys(i)-Yc) -(Zs(i)-Zc)]*[1./sum(Es.*A) 0 0;0 Kyy -Kyz; 0 -Kyz Kzz]*[0;Mz;-My];
end
fplot(Sxx,[0 L])
legend('Stringer 1','Stringer 2','Stringer 3','Stringer 4')
xlabel('Half-Span (inch)')
ylabel('Stringer Stress Distribution (Ksi)')
Sxxroot=double(subs(Sxx,x,0));
STstar=min([SyTs./SFy; SuTs./SFu],[],1)./1000;
SCstar=max([SyCs./SFy; SuCs./SFu],[],1)./1000;
for i=1:4
if Sxxroot(i)>=0
Sstar(i)=STstar(i);
else
Sstar(i)=SCstar(i);
end
end
MS=Sstar./Sxxroot-1;
SSARO=[Sxxroot;STstar;SCstar;MS];%in Ksi
Vy=Roy -int(py0+pyr.*(x./L).^rth,0,x);
Vz=Roz -int( pz0+pz2.*(x./L).^2+pz4.*(x./L).^4-ws.*nLF,0,x);
Mx=Mxo -int(-(pz0+pz2.*(x./L).^2+pz4.*(x./L).^4).*(Yc-c./4)-(py0+pyr.*(x./L).^rth).*(Zs(1)-Zc)-ws.*nLF.*(c./2-Yc)+mx0,0,x);
VzEIYY_2=(Vz*Kzz-Vy*Kyz)*...
[0;...
Es(2)*As(2)*(Zs(2)-Zc);...
Es(3)*As(3)*(Zs(3)-Zc);...
Es(4)*As(4)*(Zs(4)-Zc)];
VyEIZZ_2=(Vy*Kyy-Vz*Kyz)*...
[0;...
Es(2)*As(2)*(Ys(2)-Yc);...
Es(3)*As(3)*(Ys(3)-Yc);...
Es(4)*As(4)*(Ys(4)-Yc)];
q_1234_total= inv(K_n1)*VzEIYY_2+inv(K_n1)*VyEIZZ_2+inv(K_n1)*[Mx+Rz*(Yc-Ys(2))-Ry*(Zc-Zs(1));0;0;0];
TAO_xy_grad=[q_1234_total(1)/T_sk(1);q_1234_total(2)/T_sk(2);q_1234_total(3)/T_sk(3);q_1234_total(4)/T_sk(4)]./1000;
Tao_xy=double(subs(TAO_xy_grad,0))';
Tao_star=min([tau_u_sk./SFu ;tau_y_sk./SFy],[],1)/1000;
MS_Tao=abs(Tao_star./Tao_xy)-1;
WSSARO=[Tao_xy;Tao_star;MS_Tao];
figure(401)
clf
hold on
grid on
fplot(TAO_xy_grad,[0 L])
legend('Skin 1.2','Skin 2.3','Skin 3.4','Skin 4.1')
xlabel('Half-Span (inch)')
ylabel('Wing Skin Stress Distribution (Ksi)')
%WING TIP DISPLACEMENT DISTRIBBUTIONS
syms x
disp_V=int(int(Mz,0,x),0,x)*Kyy+int(int(My,0,x),0,x)*Kyz;
figure(501)
clf
hold on
grid on
fplot(disp_V,[0 L])
xlabel('Half-Span (inch)')
ylabel('Wing Tip Displacement (inch)')
V_tip=double(subs(disp_V,L));
disp_W=int(int(-My,0,x),0,x)*Kzz+int(int(-Mz,0,x),0,x)*Kyz;
fplot(disp_W,[0 L])
legend('In-plane Displacement','Transverse Displacement')
W_tip=double(subs(disp_W,L));
%twist
q_1234_total_3= inv(K_n1)*VzEIYY_2+inv(K_n1)*VyEIZZ_2+inv(K_n1)*[Mx+Rz*(Yc-Ys(2))-Ry*(Zc-Zs(1));0;0;0];
Twist_eq=180/pi*int(1/(2*sum(A))*sum(q_1234_total_3'.*S./G_sk./T_sk),0,x);
figure(503)
clf
hold on
grid on
fplot(Twist_eq,[0 L])
xlabel('Half-Span (inch)')
ylabel('Twist Distribution (degrees)')
theta_tip1=double(subs(Twist_eq,L));
WTDaT=[W_tip;V_tip;theta_tip1];
%write to exel
xlswrite(outFile, WCSP , 1, 'G68:G76' );
xlswrite(outFile, ISR_Root , 1, 'G151:G156' );
xlswrite(outFile, SSARO , 1, 'G277:J280' );
xlswrite(outFile, WSSARO , 1, 'G308:J310' );
xlswrite(outFile, WTDaT , 1, 'G338:G340' );
createFigure(outFile,1,101,'E80','O100');
createFigure(outFile,1,102,'E103','O123');
createFigure(outFile,1,103,'E126','O146');
createFigure(outFile,1,201,'E160','O180');
createFigure(outFile,1,202,'E183','O203');
createFigure(outFile,1,203,'E206','O226');
createFigure(outFile,1,204,'E229','O249');
createFigure(outFile,1,205,'E252','O272');
createFigure(outFile,1,301,'E283','O303');
createFigure(outFile,1,401,'E313','O333');
createFigure(outFile,1,501,'E344','O364');
createFigure(outFile,1,503,'E367','O387');
% End of Function: wingAnalysis
% ------------------------------------------------------------------------
end